Search algorithms
In this lesson, we'll do a brief recap about search algorithms with which we're already familiar (depth-first search and breadth-first search), and use those as a launchpoint to talk about a "smarter" search algorithm called A* search (pronounced "A-star").
This lesson is not quite an object-oriented programming lesson per se. It's definitely very specifically tied to one of the programming projects.
In your previous class (for many of you, CSC 202 Data Structures), you learned about the general tree data structure. A tree is hierarchical data structure, made up of a root node that has zero or more child nodes, each of which is a tree (or a "subtree").
For example, this is a tree:
graph TD;
A((A))
B((B))
C((C))
D((D))
E((E))
F((F))
G((G))
A-->B;
A-->C;
B-->D;
B-->E;
C-->F;
C-->G;
One of the many operations you can perform in trees is to search for a particular value, using some search algorithm.
For example, we may want to find a path from the root of the tree (A) to a particular target node (say, E).
The anatomy of a search
Two search algorithms that you may already be familiar with are depth-first search (DFS) and breadth-first search (BFS).
A depth-first search proceeds by exploring (or "visiting") the root node first, then recursively searching each subtree. The following animation from Wikipedia illustrates it well:
By Mre - Own work, CC BY-SA 3.0, Link
In contrast, a breadth-first search proceeds by visiting all nodes at a given level (or "depth") before moving on to nodes at the next level.
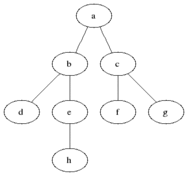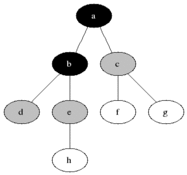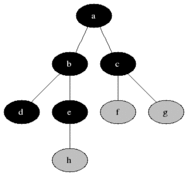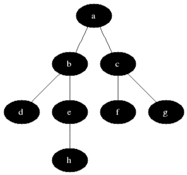
By Blake Matheny, CC BY-SA 3.0
Both DFS and BFS can be described with the following structure:
- First, know your
startNodeand yourtargetNode. - Initialize a "to-do list" of nodes that need to be explored during the search. This is also sometimes called the "frontier".
- Add your
startNodeto the "to-do" list—it's the first thing that'll be explored. - While your to-do list is not empty:
- Remove the next node from the to-do list.
- Is it the
targetNode? If so, you're done! - If it's not the
targetNode, add its children to the to-do list. - Run this loop again.
- If you end the loop without having found
targetNode, then it must not be reachable fromstartNode.
Or, expressed in pseudocode:
1. | function search(startNode, targetNode) {
2. | initialize todoList;
3. | add startNode to todoList;
4. | while (todoList is not empty) {
5. | currentNode = remove next node from todoList;
6. | if (currentNode == targetNode) {
7. | return "found!";
8. | }
9. | add children of currentNode to todoList;
10.| }
11.| return "not found";
12.| }
The only difference between DFS and BFS is the order in which the "next" node is removed from the to-do list.
That is, on line 5 above, if we remove the most recently-added node from the to-do list, then we're doing a depth-first search (because we go deep into one branch before exploring others). If we remove the least-recently-added node from the to-do list, then we're doing a breadth-first search (because we explore all nodes at the current depth before going deeper).
Another way to think about this is: in DFS, the to-do list is a stack data structure (last-in, first-out), while in BFS, the to-do list is a queue data structure (first-in, first-out).
Search in a graph
Searches in graphs require a small but crucial modification to the general search algorithm above.
The steps above are sufficient for searches in tree data structures. However, in this lesson, we will be focusing on searches in graph data structures.
A graph is a set of nodes (also called vertices) connected by edges. There are key differences between trees and graphs. In graphs,
- there's no fixed "root" node. Typically, a "search" in a graph starts from some arbitrarily chosen
startNode. - nodes can be connected in arbitrary ways, as opposed to the hierarchical parent-child relationship seen in trees.
For example, this is a graph, but not a tree:
graph LR;
A((A))
B((B))
C((C))
D((D))
E((E))
A---B;
A---C;
B---D;
C---D;
D---E;
C---E;
Crucially, in graphs, there may be cycles.
Cycles occur when a node is reachable from itself by following a sequence of edges.
In the example above, we can start at A, and take a series of edges to get back to A again: A -> B -> D -> C -> A.
Activity
Let's run through our general search algorithm using the graph above.
We'll start from node A and try to search for node E.
Let's use BFS.
We'll by marking E as our target, and adding A to our to-do list, which is a queue (because BFS).
graph LR;
A((A)):::frontier
B((B))
C((C))
D((D))
E((E)):::target
A---B;
A---C;
B---D;
C---D;
D---E;
C---E;
classDef target fill:#10b981,stroke:#059669,stroke-width:3px,color:#000
classDef visited fill:#7c3aed,stroke:#5b21b6,stroke-width:2px,color:#fff
classDef current fill:#f59e0b,stroke:#d97706,stroke-width:4px,color:#000
classDef frontier fill:#06b6d4,stroke:#0891b2,stroke-width:2px,color:#000
- target
- current node
- to-do list
To-do list (added A):
| → | A | → |
Our next step is to dequeue A from the to-do list. It is now our current node. It's not our target, so we enqueue its neighbours, B and C.
graph LR;
A((A)):::current
B((B)):::frontier
C((C)):::frontier
D((D))
E((E)):::target
A---B;
A---C;
B---D;
C---D;
D---E;
C---E;
classDef target fill:#10b981,stroke:#059669,stroke-width:3px,color:#000
classDef visited fill:#7c3aed,stroke:#5b21b6,stroke-width:2px,color:#fff
classDef current fill:#f59e0b,stroke:#d97706,stroke-width:4px,color:#000
classDef frontier fill:#06b6d4,stroke:#0891b2,stroke-width:2px,color:#000
- target
- current node
- to-do list
To-do list (removed A, added B and C):
| → | C | B | → |
Now, we'll dequeue B from the to-do list, because it was "first in", and explore it.
Again, exploring it means adding its neighbours to the to-do list.
At this point, we have a problem.
When we explore B, and try to add its neighbours to our to-do list, we would correctly enqueue D. But because A is also a neighbour of B, we'd end up re-adding A to the list!
Even if we didn't re-add A now, we would re-add it later when we explore C, which is also a neighbour of A.
graph LR;
A((A)):::frontier
B((B)):::current
C((C)):::frontier
D((D)):::frontier
E((E)):::target
A---B;
A---C;
B---D;
C---D;
D---E;
C---E;
classDef target fill:#10b981,stroke:#059669,stroke-width:3px,color:#000
classDef visited fill:#7c3aed,stroke:#5b21b6,stroke-width:2px,color:#fff
classDef current fill:#f59e0b,stroke:#d97706,stroke-width:4px,color:#000
classDef frontier fill:#06b6d4,stroke:#0891b2,stroke-width:2px,color:#000
- target
- current node
- to-do list
To-do list (removed B, added D and A):
| → | D | A | C | → |
Eventually, this would cause us to re-visit A, which in turn would re-add B to the to-do list, which would re-add A, and so on.
Because of this, our search would just ping-pong between A and B forever, never reaching our target E.
To avoid this in a graph with cycles, we need to also keep track of which nodes we've already visited. Let's revisit our "anatomy of a search" pseudocode. See lines 9 and 10 in our updated pseudocode.
(Note that this assumes a node cannot be its own neighbour.)
1. | function search(startNode, targetNode) {
2. | initialize todoList;
3. | add startNode to todoList;
4. | while (todoList is not empty) {
5. | currentNode = remove next node from todoList;
6. | if (currentNode == targetNode) {
7. | return "found!";
8. | }
9. | add ONLY UNVISITED children of currentNode to todoList;
10.| mark currentNode as visited;
11.| }
12.| return "not found";
13.| }
Here's how our search would progress with this modification.
graph LR;
A((A)):::frontier
B((B))
C((C))
D((D))
E((E)):::target
A---B;
A---C;
B---D;
C---D;
D---E;
C---E;
classDef target fill:#10b981,stroke:#059669,stroke-width:3px,color:#000
classDef visited fill:#7c3aed,stroke:#5b21b6,stroke-width:2px,color:#fff
classDef current fill:#f59e0b,stroke:#d97706,stroke-width:4px,color:#000
classDef frontier fill:#06b6d4,stroke:#0891b2,stroke-width:2px,color:#000
- target
- current node
- to-do list
To-do list (added A):
| → | A | → |
Next, we make A our current node by dequeing it and enqueing its neighbours:
graph LR;
A((A)):::current
B((B)):::frontier
C((C)):::frontier
D((D))
E((E)):::target
A---B;
A---C;
B---D;
C---D;
D---E;
C---E;
classDef target fill:#10b981,stroke:#059669,stroke-width:3px,color:#000
classDef visited fill:#7c3aed,stroke:#5b21b6,stroke-width:2px,color:#fff
classDef current fill:#f59e0b,stroke:#d97706,stroke-width:4px,color:#000
classDef frontier fill:#06b6d4,stroke:#0891b2,stroke-width:2px,color:#000
- target
- current node
- to-do list
To-do list (removed A, added B and C):
| → | C | B | → |
The big addition here is that we now mark A as visited before picking up one of its neighbours to search next.
graph LR;
A((A)):::visited
B((B)):::frontier
C((C)):::frontier
D((D))
E((E)):::target
A---B;
A---C;
B---D;
C---D;
D---E;
C---E;
classDef target fill:#10b981,stroke:#059669,stroke-width:3px,color:#000
classDef visited fill:#7c3aed,stroke:#5b21b6,stroke-width:2px,color:#fff
classDef current fill:#f59e0b,stroke:#d97706,stroke-width:4px,color:#000
classDef frontier fill:#06b6d4,stroke:#0891b2,stroke-width:2px,color:#000
- target
- current node
- to-do list
- visited
To-do list:
| → | C | B | → |
We can now proceed to dequeue B, explore it, and add its unvisited neighbour D to the to-do list (but not A, since it's already been visited):
graph LR;
A((A)):::visited
B((B)):::current
C((C)):::frontier
D((D)):::frontier
E((E)):::target
A---B;
A---C;
B---D;
C---D;
D---E;
C---E;
classDef target fill:#10b981,stroke:#059669,stroke-width:3px,color:#000
classDef visited fill:#7c3aed,stroke:#5b21b6,stroke-width:2px,color:#fff
classDef current fill:#f59e0b,stroke:#d97706,stroke-width:4px,color:#000
classDef frontier fill:#06b6d4,stroke:#0891b2,stroke-width:2px,color:#000
- target
- current node
- to-do list
- visited
To-do list (removed B; added D, but not A):
| → | D | C | → |
The search can now make forward progress instead of going in circles. Hurray!
We now mark B as visited, and pick up C, since that's first in our queue.
C has three neighbours: A (already visited), D (in the to-do list already), and E (our target!).
We will add only E to the to-do list (but we won't change its colour in the graph below—don't want you forgetting that its our target!).
graph LR;
A((A)):::visited
B((B)):::visited
C((C)):::current
D((D)):::frontier
E((E)):::target
A---B;
A---C;
B---D;
C---D;
D---E;
C---E;
classDef target fill:#10b981,stroke:#059669,stroke-width:3px,color:#000
classDef visited fill:#7c3aed,stroke:#5b21b6,stroke-width:2px,color:#fff
classDef current fill:#f59e0b,stroke:#d97706,stroke-width:4px,color:#000
classDef frontier fill:#06b6d4,stroke:#0891b2,stroke-width:2px,color:#000
- target
- current node
- to-do list
- visited
To-do list (removed C; added E):
| → | E | D | → |
Next, we'll mark C as visited, and dequeue D from the to-do list.
graph LR;
A((A)):::visited
B((B)):::visited
C((C)):::visited
D((D)):::current
E((E)):::target
A---B;
A---C;
B---D;
C---D;
D---E;
C---E;
classDef target fill:#10b981,stroke:#059669,stroke-width:3px,color:#000
classDef visited fill:#7c3aed,stroke:#5b21b6,stroke-width:2px,color:#fff
classDef current fill:#f59e0b,stroke:#d97706,stroke-width:4px,color:#000
classDef frontier fill:#06b6d4,stroke:#0891b2,stroke-width:2px,color:#000
- target
- current node
- to-do list
- visited
To-do list (removed D):
| → | E | → |
D has no neighbours that need further action, and the only node left in our to-do list is E, which is our target!
We finish by dequeuing E, exploring it, and finding that it is indeed our target node.
graph LR;
A((A)):::visited
B((B)):::visited
C((C)):::visited
D((D)):::visited
E((E)):::target
A---B;
A---C;
B---D;
C---D;
D---E;
C---E;
classDef target fill:#10b981,stroke:#059669,stroke-width:3px,color:#000
classDef visited fill:#7c3aed,stroke:#5b21b6,stroke-width:2px,color:#fff
classDef current fill:#f59e0b,stroke:#d97706,stroke-width:4px,color:#000
classDef frontier fill:#06b6d4,stroke:#0891b2,stroke-width:2px,color:#000
- target
- current node
- to-do list
- visited
To-do list is empty
Success!
We've just walked through a breadth-first search in a graph with cycles, using a to-do list (queue) to manage the nodes we have yet to visit, and also some mechanism to track which nodes we've already visited.
PONDER
Here are two questions to think about (and unlike the rest of this chapter, these are software design questions):
- How would you manage visited nodes in an actual implementation of this algorithm?
- Right now, all we can say is "yes, we found it". But a more useful search function would give back a path from
startNodetotargetNode. How would you modify the algorithm to do that? What additional data structures or information would you need to keep track of?
Some interactive examples
Ok, we have the basic idea of DFS and BFS down. Let's see what those algorithms look like in a 2-dimensional grid environment.
First, recognise that we can think of the grid as a graph. Each square in the grid is a node, and each node is connected to its neighbours (up, down, left, right).
DFS (Depth-First Search)
The interactive widget below lets you visualize a depth-first search in action in a grid-like environment. You can use your mouse to drag the start point (green square) and the target point (red square) to different locations on the grid, or click "Shuffle grid" to randomize their locations.
When you're ready, click "Toggle Search" to start the search.
DFS looks...kind of crazy in a grid, because it goes as deep as possible in one direction before backtracking. It is not very efficient in a grid, because so much depends on the order in which directions are explored.
(In this example, the order is top, right, bottom, left.)
We're just not gonna talk more about DFS here.
BFS (Breadth-First Search)
The interactive widget below lets you visualize a breadth-first search in action.
In a tree, BFS looks like a "level-order" search; in a grid, it looks like concentric circles expanding outwards from the start point.
Notice the limitations of BFS in a grid environment: it explores a lot of unnecessary nodes, especially when the start and target points are far apart.
For example, drag the points so that the end node is directly to the right of the start node, a few spaces away. We can see that the shortest path is a straight line to the right, but BFS still explores all the nodes above and below that line.
We have information about where the target is (its x-y coordinates), but BFS doesn't use it! That is because BFS naively uses a first-in, first-out queue to explore nodes, without any regard for their actual distance from the target.
Can we do better?
A* Search
That is where A* (A-star) search comes in.
A* search is like a "smarter" version of BFS; instead of a simple first-in, first-out queue, it uses a priority queue to explore nodes that are "closer" to the target first.
The best way to see this in action is to use the interactive widget below.
Align the start and goal points so they're a few spaces apart in a straight line, and see how A* search doesn't waste time searching all around itself, and instead heads straight for the target.
As another example, drag the goal point so it's not in a straight line from the start point. See how A* search still heads generally in the right direction. For example, if the goal is upward and to the right of the start point, our visited nodes might still look somewhat like a BFS, except we will avoid searching obviously-wrong directions (like downwards or to the left).
So how does A* search work?
Ok, so we have a vague sense that A* search is better than BFS, because it'll likely search fewer nodes due to its use of a priority queue. But how is the priority queue making ordering decisions? How does it decide what the best "next steps" are?
The A* algorithm keeps track of two pieces of information for each node: the g-value and the h-value (defined below).
The priority of a node is determined by the sum of its g-value and h-value, often called the f-value. Nodes with lower f-values are given higher priority, and are therefore removed from the priority queue first.
The g-value
This is the number of steps taken to get from the start node to the current node. As you consider a node for addition to the priority queue, you can compute this value by taking the g-value of its previous node and adding 1.
So, for example:
- You start at the
start. Its g-value is 0. - The
startnode will have four neighbours (assuming it's not at the edge of the grid and none of its neighbours are obstacles). Each of those neighbours will have a g-value of 1 (one step from the start). - Those neighbours will themselves have neighbours, each with a g-value of 2 (two steps from the start), and so on.
However, consider that there may be obstacles in the grid that prevent direct movement. In that scenario, the g-value will reflect the actual number of steps taken to reach a node, not just the straight-line distance.
So, for example, you might have a node that's physically 2 steps away from start (based purely on mathematical differences in their coordinates). But, if there are obstacles in the way, and your search took 5 steps to reach that node, then that node's g-value is 5.
The h-value
The second bit of information that we keep track of for each node is its h-value, also called the heuristic value.
This is the estimated number of steps needed to get from the current node to the goal node.
This is usually computed using some distance metric, like Manhattan distance or Euclidean distance.
The Manhattan distance between two points p1 and p2 is computed as Math.abs(p1.x - p2.x) + Math.abs(p1.y - p2.y).
Intuitively, it's the number of steps you would need to take to get from p1 to p2, moving only in straight lines along the grid.
So in the grid below, the Manhattan distance from A to B is 4. Most directly, this could be achieved by moving 2 steps down and 2 steps right, or 2 steps right and 2 steps down. Or you could move 1 step down, 2 steps right, and 1 step down. Either way, the total number of steps is 4.
| A | . | . |
| . | . | . |
| . | . | B |
Euclidean distance is computed as Math.sqrt(Math.pow(p1.x - p2.x, 2) + Math.pow(p1.y - p2.y, 2)) or \( \sqrt{(p1_{x} - p2_{x})^2 + (p1_{y} - p2_{y})^2} \)
Intuitively, it's the straight-line distance between p1 and p2.
Euclidean distance may be useful if diagonal movement is allowed in the grid.
In our examples, we're only moving in straight lines, so we'll use Manhattan distance as our heuristic.
Putting it together
When considering which node to explore next, A* search computes the f-value for each node in the priority queue as f = g + h.
Each node's f-value can be thought of as "the estimated total cost of a path that goes through this node". It includes the known number of steps taken to get here (g-value) and the estimated number of steps needed to reach the goal (h-value).
The algorithm
- Know the
startandgoalnodes. - Initialize a priority queue (the to-do list). This is often called the "open list".
- Initialize a set to keep track of visited nodes. This is often called the "closed set" or "closed list".
- Add the
startnode to the priority queue, with a g-value of 0 and an h-value computed using the heuristic function, i.e.,manhattan(start, goal). - While the priority queue is not empty:
- Remove the node with the lowest f-value from the priority queue. This is the current node.
- If the current node is the
goalnode, the search is done. Think about how you would reconstruct the path fromstarttogoalat this point. - For each unvisited neighbour of the current node:
- Compute its g-value as
current.g + 1. - Compute its h-value using the heuristic function, i.e.,
manhattan(neighbour, goal). - Check if the neighbour is already in the priority queue. (This can happen if you reach a neighbour multiple times via different paths.)
- If the neighbour is not already in the priority queue, add it with its computed g and h values.
- If the neighbour is already in the priority queue, but the new g-value is lower than its existing g-value, update its g and h values in the priority queue. (In practice, this will require removing and re-adding the node to the priority queue to maintain the correct ordering.)
- Compute its g-value as
- Mark the current node as visited (i.e., add it to the closed list).
But wait! Obstacles
A* search looks miles better than BFS in a grid without obstacles. However, even more interesting is how A* search performs in a grid with obstacles. Scroll up or click the link to go to the interactive widget for A-star search.
Click and drag across the grid to add obstacles (grey squares). Obstacles are nodes that cannot be explored or traversed. Try placing obstacles in various configurations, for example:
- Place obstacles right around the start point, forcing the search to find a way out.
- Place obstacles around (but not completely blocking) the goal point, forcing the search to find a way in. In particular, note how A*'s use of a heuristic helps it head directly for the goal rather optimistically—until it hits a road block and has to find a way around it.
- What happens when you block off any access to the goal point?